Zhu, Siegel, Mitman, Isi, et al. (2025). Black Hole Spectroscopy for Precessing Binary Black Hole Coalescences. Phys. Rev. D 111, 6, p. 064052. arXiv:2312.08588.
All Publications
Mitman, Pretto, Siegel, Scheel, et al. (2025). Probing the ringdown perturbation in binary black hole coalescences with an improved quasi-normal mode extraction algorithm. Submitted to Phys. Rev. D. arXiv:2503.09678.
Re, Mitman, Stein, Scheel, et al. (2025). Modeling the BMS transformation induced by a binary black hole merger. Submitted to Phys. Rev. D. arXiv:2503.09569.
Deppe, Heisenberg, Kidder, Maibach, et al. (2025). Signatures of Quantum Gravity in Gravitational Wave Memory. Submitted to Phys. Rev. D. arXiv:2502.20584.
Gao, Cook, Kidder, Pfeiffer, et al. (2025). The robustness of extracting quasinormal mode information from black hole merger simulations. Submitted to Phys. Rev. D. arXiv:2502.15921.
Ma, Nelli, Moxon, Scheel, et al. (2025). Einstein-Klein-Gordon system via Cauchy-characteristic evolution: Computation of memory and ringdown tail. Class. Quant. Grav. 42, 5, p. 055006. arXiv:2409.06141.
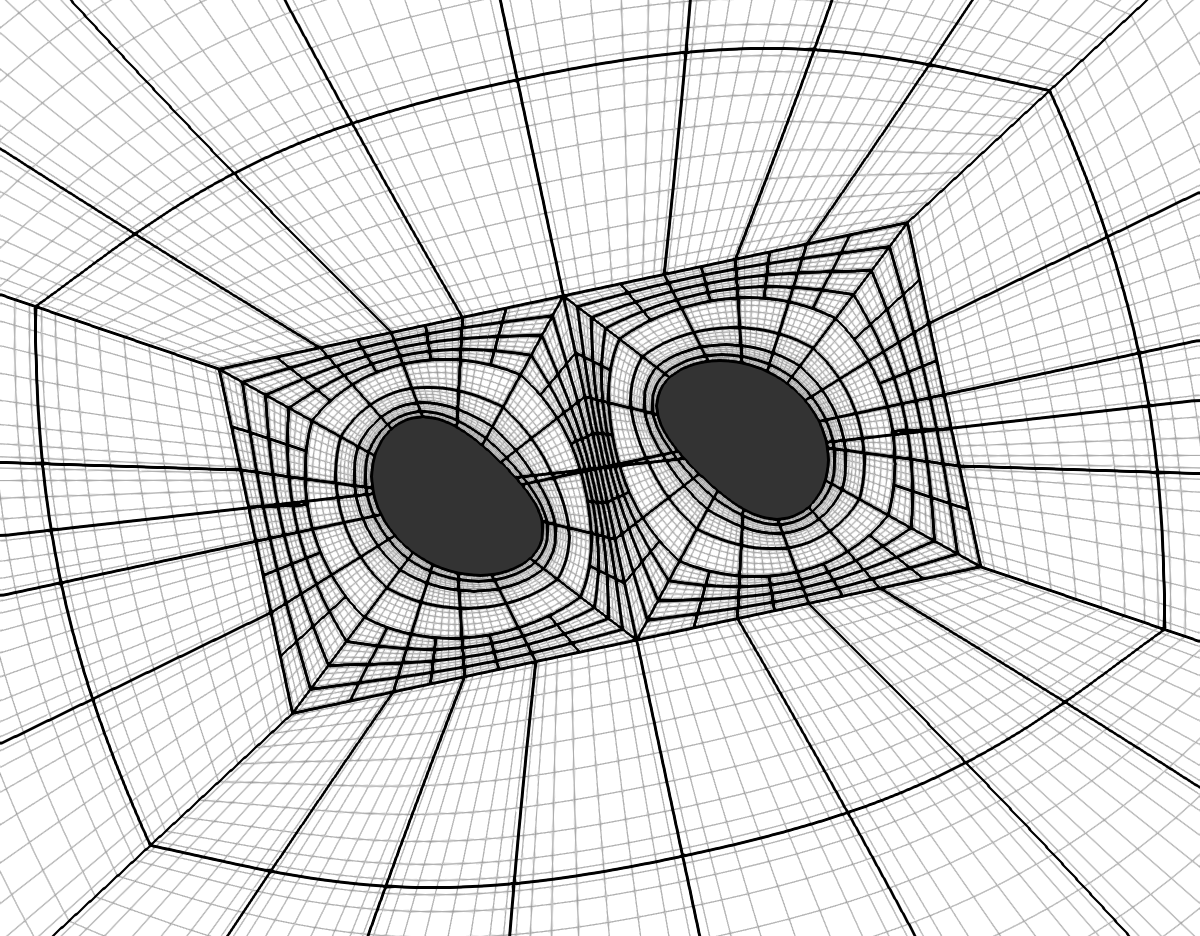
Lovelace, Nelli, Deppe, Vu, et al. (2025). Simulating binary black hole mergers using discontinuous Galerkin methods. Class. Quant. Grav. 42, 3, p. 035001. arXiv:2410.00265.

Nee, Lara, Pfeiffer, and Vu (2025). Quasistationary hair for binary black hole initial data in scalar Gauss-Bonnet gravity. Phys. Rev. D 111, 2, p. 024061. arXiv:2406.08410.
Ma, Scheel, Moxon, Nelli, et al. (2024). Merging black holes with Cauchy-characteristic matching: Computation of late-time tails. Submitted to Phys. Rev. D. arXiv:2412.06906.
Amicis, Rüter, Carullo, Albanesi, et al. (2024). Late-time tails in nonlinear evolutions of merging black holes. Submitted to Phys. Rev. D. arXiv:2412.06887.
Giesler, Ma, Mitman, Oshita, et al. (2024). Overtones and Nonlinearities in Binary Black Hole Ringdowns. Submitted to Phys. Rev. D. arXiv:2411.11269.
Deppe, Foucart, Bonilla, Boyle, et al. (2024). Binary neutron star mergers using a discontinuous Galerkin-finite difference hybrid method. Class. Quant. Grav. 41, 24, p. 245002. arXiv:2406.19038.
Deppe, Heisenberg, Inchauspé, Kidder, et al. (2024). Echoes from Beyond: Detecting Gravitational Wave Quantum Imprints with LISA. Submitted to Phys. Rev. Lett. arXiv:2411.05645.

Wittek, Barack, Pfeiffer, Pound, et al. (2024). Relieving scale disparity in binary black hole simulations. Submitted to Phys. Rev. Lett. arXiv:2410.22290.

Vu (2024). Discontinuous Galerkin scheme for elliptic equations on extremely stretched grids. Phys. Rev. D 110, 8, p. 084062. arXiv:2405.06120.
Mitman, Boyle, Stein, Deppe, et al. (2024). A Review of Gravitational Memory and BMS Frame Fixing in Numerical Relativity. Class. Quant. Grav. 41, 22, p. 223001. arXiv:2405.08868.
Chen, Boyle, Deppe, Kidder, et al. (2024). Improved frequency spectra of gravitational waves with memory in a binary-black-hole simulation. Phys. Rev. D 110, 6, p. 064049. arXiv:2405.06197.
Zertuche, Stein, Mitman, Field, et al. (2024). High-Precision Ringdown Surrogate Model for Non-Precessing Binary Black Holes. arXiv:2408.05300.

Lara, Pfeiffer, Wittek, Vu, et al. (2024). Scalarization of isolated black holes in scalar Gauss-Bonnet theory in the fixing-the-equations approach. Phys. Rev. D 110, 2, p. 024033. arXiv:2403.08705.
Ma, Moxon, Scheel, Nelli, et al. (2024). Fully relativistic three-dimensional Cauchy-characteristic matching for physical degrees of freedom. Phys. Rev. D 109, 12, p. 124027. arXiv:2308.10361.
Clarke, Isi, Lasky, Thrane, et al. (2024). Toward a self-consistent framework for measuring black hole ringdowns. Phys. Rev. D 109, 12, p. 124030. arXiv:2402.02819.
Zhu, Ripley, Pretorius, Ma, et al. (2024). Nonlinear effects in black hole ringdown from scattering experiments: Spin and initial data dependence of quadratic mode coupling. Phys. Rev. D 109, 10, p. 104050. arXiv:2401.00805.
Pompili, Buonanno, Estellés, Khalil, et al. (2023). Laying the foundation of the effective-one-body waveform models SEOBNRv5: improved accuracy and efficiency for spinning non-precessing binary black holes. Phys. Rev. D 108, 12, p. 124035. arXiv:2303.18039.
Deppe, Kidder, Teukolsky, Bonilla, et al. (2023). A positivity-preserving adaptive-order finite-difference scheme for GRMHD. Class. Quantum Grav. 40, p. 245014. arXiv:2306.04755.
Boschini, Gerosa, Varma, Armaza, et al. (2023). Extending black-hole remnant surrogate models to extreme mass ratios. Phys. Rev. D 108, 8, p. 084015. arXiv:2307.03435.
Yoo, Mitman, Varma, Boyle, et al. (2023). Numerical relativity surrogate model with memory effects and post-Newtonian hybridization. Phys. Rev. D 108, 6, p. 064027. arXiv:2306.03148.
Wittek, Dhesi, Barack, Pfeiffer, et al. (2023). Worldtube excision method for intermediate-mass-ratio inspirals: scalar-field model in 3+1 dimensions. Phys. Rev. D 108, 2, p. 024041. arXiv:2304.05329.
Moxon, Scheel, Teukolsky, Deppe, et al. (2023). SpECTRE Cauchy-characteristic evolution system for rapid, precise waveform extraction. Phys. Rev. D 107, 6, p. 064013. arXiv:2110.08635.
Mitman, Lagos, Stein, Ma, et al. (2023). Nonlinearities in black hole ringdowns. Phys. Rev. Lett. 130, 8, p. 081402. arXiv:2208.07380.
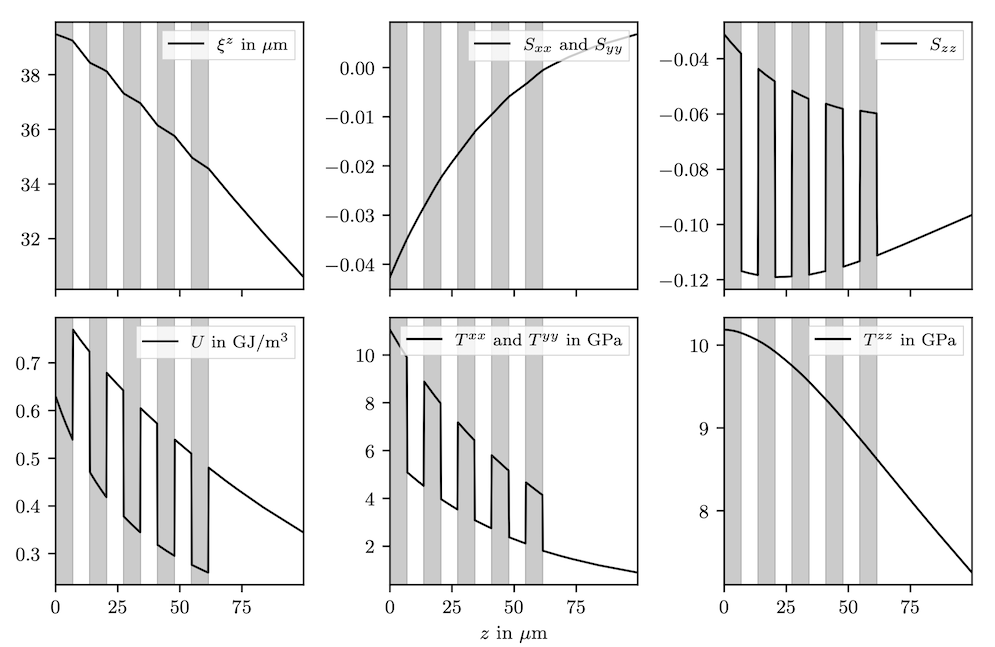
Vu, Rodriguez, Wlodarczyk, Lovelace, et al. (2023). High-accuracy numerical models of Brownian thermal noise in thin mirror coatings. Class. Quantum Grav. 40, p. 025015. arXiv:2111.06893.
Ma, Mitman, Sun, Deppe, et al. (2022). Quasinormal-mode filters: A new approach to analyze the gravitational-wave ringdown of binary black-hole mergers. Phys. Rev. D 106, 8, p. 084036. arXiv:2207.10870.
Mitman, Stein, Boyle, Deppe, et al. (2022). Fixing the BMS frame of numerical relativity waveforms with BMS charges. Phys. Rev. D 106, 8, p. 084029. arXiv:2208.04356.
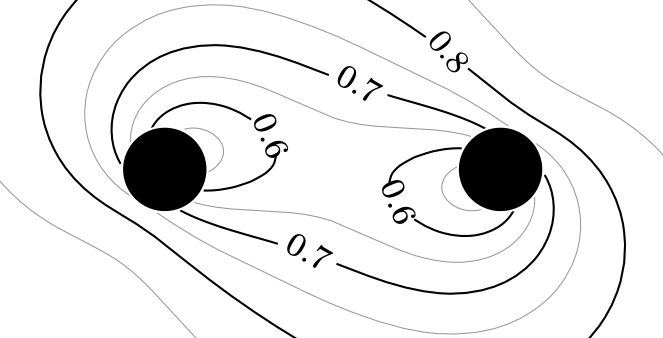
Vu (2022). A task-based parallel elliptic solver for numerical relativity with discontinuous Galerkin methods. Universität Potsdam:10.25932/publishup-56226.
Deppe, Hébert, Kidder, Throwe, et al. (2022). Simulating magnetized neutron stars with discontinuous Galerkin methods. Phys. Rev. D 105, 12, p. 123031. arXiv:2109.12033.
Zertuche, Mitman, Khera, Stein, et al. (2022). High Precision Ringdown Modeling: Multimode fits and BMS frames. Phys. Rev. D 105, 10, p. 104015. arXiv:2110.15922.
Ma, Wang, Deppe, Hébert, et al. (2022). Gravitational-wave echoes from numerical-relativity waveforms via spacetime construction near merging compact objects. Phys. Rev. D 105, 10, p. 104007. arXiv:2203.03174.
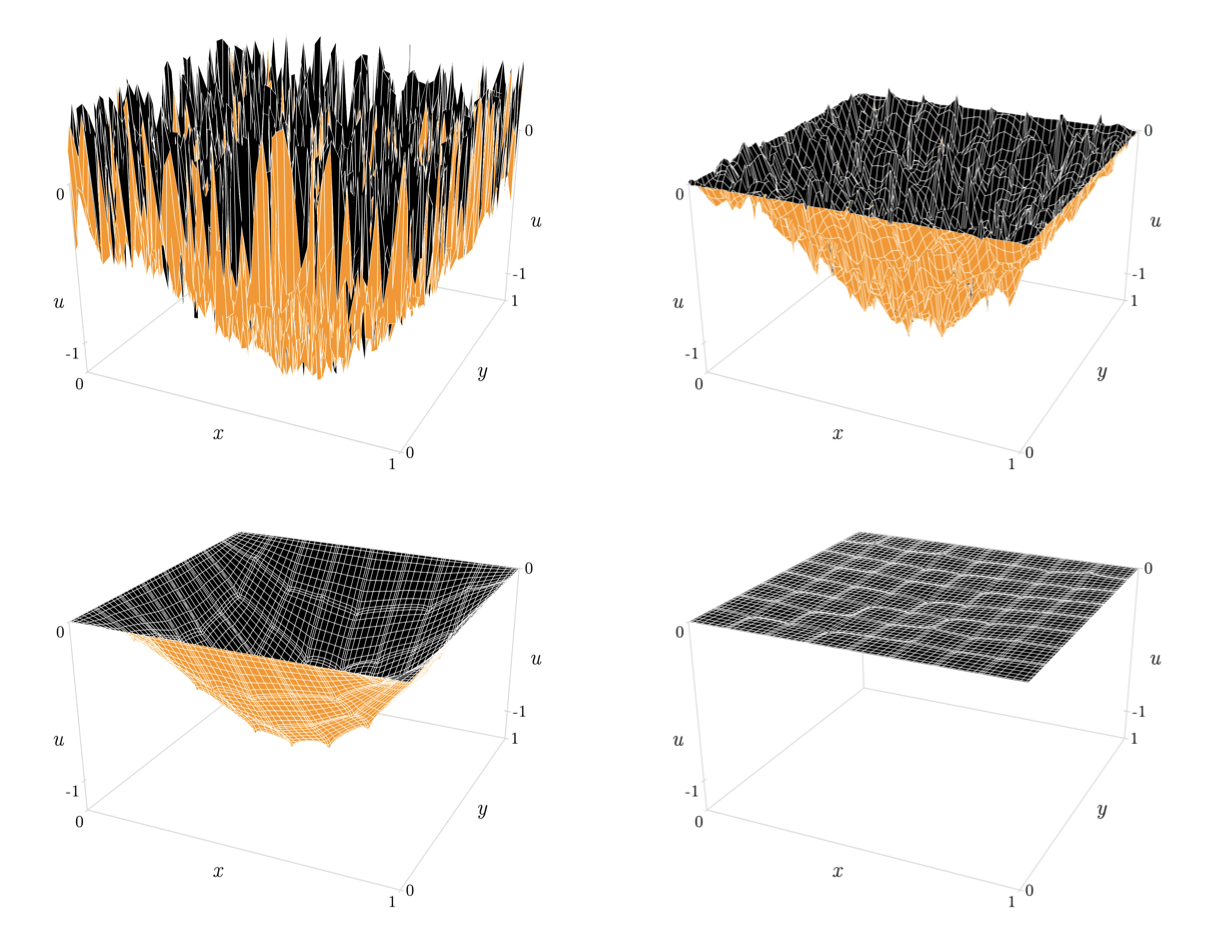
Vu, Pfeiffer, Bonilla, Deppe, et al. (2022). A scalable elliptic solver with task-based parallelism for the SpECTRE numerical relativity code. Phys. Rev. D 105, 8, p. 084027. arXiv:2111.06767.

Fischer and Pfeiffer (2022). Unified discontinuous Galerkin scheme for a large class of elliptic equations. Phys. Rev. D 105, 2, p. 024034. arXiv:2108.05826.
Düll, Fischer, Schaefer, and Schuller (2020). Symmetric gravitational closure. arXiv:2003.07109.
Vincent, Pfeiffer, and Fischer (2019). hp-adaptive discontinuous Galerkin solver for elliptic equations in numerical relativity. Phys. Rev. D 100, 8. arXiv:1907.01572.
Boyle, Hemberger, Iozzo, Lovelace, et al. (2019). The SXS collaboration catalog of binary black hole simulations. Class. Quantum Grav. 36, 19, p. 195006. arXiv:1904.04831.
Kuznetsov, Fischer, and Guo (2018). The Archive Solution for Distributed Workflow Management Agents of the CMS Experiment at LHC. Computing and Software for Big Science 2, 1. arXiv:1801.03872.